期刊VIP學術指導 符合學術規范和道德
保障品質 保證專業,沒有后顧之憂
期刊VIP學術指導 符合學術規范和道德
保障品質 保證專業,沒有后顧之憂
摘 要:針對提高多關節機械臂軌跡規劃精準率和效率的問題,利用Peter Corke開發的robotics-toolbox工具箱在MATLAB上進行機械臂的運動學建模,并設計了一種軌跡規劃算法。該算法依托于LM算法,結合逆運動學獲取關節角序列位置,在對應相關軌跡的同時,確保關節角速度和加速度曲線連續且光滑。研究結果表明,通過該算法不但可以得到相對穩定的運動曲線,其迭代速度相比傳統的梯度下降法,在擬合離散點過程中具有更快的迭代速度。
關鍵詞:機械臂;LM算法;軌跡規劃;MATLAB Toolbox;最小二乘法;工業互聯網;機器人
0 引言
如今隨著科技的發展,機械臂在工業生產中的地位越來越不可替代,而軌跡規劃是機械臂設計過程中的重要組成部分。一般而言,可利用機械臂的可靠性標準及效率標準評估機械臂性能,因此本文研究核心在于如何提升機械臂的可靠性以及如何改善機械臂運行效率[1]。目前,研究人員在規劃機械臂運動軌跡方面提出了很多方案,但是每種方案的指向性較強,往往僅適用于一種或少量場景,而難以在大部分場景中獲取最優解。由于存在較多優化目標,時間、能量及精準度等均是優化的切入點[2],研究人員也可選擇粒子群算法或蟻群算法等多種算法。
相對而言,國外研究人員在機械臂方面的研究處于領先地位。如Ohta等[3]設計了一種軌跡規劃方法,將最優軌跡劃分成兩部分,在離線追蹤之后恢復在線追蹤,結合機械臂的各項物理約束選擇三次樣條函數,在此基礎上對機械臂軌跡進行規劃,并基于特定算法完成相應優化,以便在最大程度上縮短實現時間。國內研究人員在相關領域也進行了廣泛研究,在算法和操作理念方面均有所創新。如田海波等[4]通過近似代換的方法,將約束邊界條件納入考量范圍,通過幾何法確定最優解,有利于實現預期優化目標。需要強調的是,通過幾何法規劃機械臂軌跡的復雜度較高,在很多場景下難以操作[5]。孫亮等[6]通過五段三次多項式軌跡獲取角速度和角加速度,為機械臂軌跡規劃提供數據支持。
4 仿真驗證
此次仿真得到的結果如圖1所示,并基于此完成模型構建。
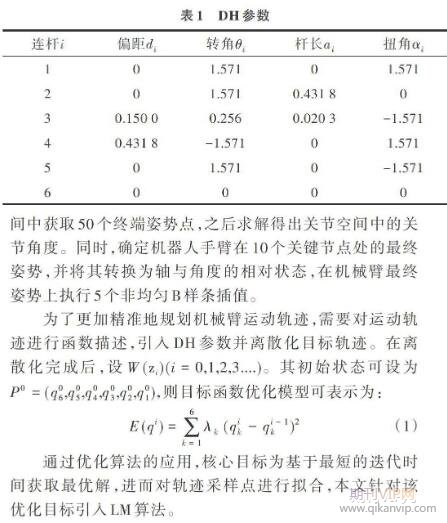
通過分析DH坐標系,可確定初始狀態相關參數[18]以及連桿系數,在此基礎上確定目標點坐標,進而利用DH坐標系計算機械臂末端狀態值,由robot-toolbox工具箱可計算得出DH參數如圖2所示。
本文得到的軌跡效果如圖3所示。
本文在不同方法對比分析的基礎上,針對機械臂軌跡規劃問題,選擇較為合適的優化方法完成迭代過程,利用MATLAB Toolbox工具箱計算得出的實時動畫與曲線圖反映迭代次數與優化結果的關系,以便整合離散數據,進而得出比較準確的仿真結果。結果顯示,在大部分時間內,尤其在20輪迭代前,梯度下降法的迭代速度遠不及LM算法,而在40輪迭代后,二者都趨于穩定。LM算法在迭代過程中表現出整體穩定的特征,但同時在某些迭代過程中會出現梯度上升的情況,這與參數初始化選擇及超參數調整有關,可通過后續調參對迭代效果作進一步優化。
5 結語
為了更好地進行機械臂軌跡規劃,同時為避免機械臂在運動過程中產生震動,影響其使用性能,在MATLAB中建立運動模型并進行實時狀態追蹤。結果顯示,在設定的運動范圍內機械臂運行平穩,運行過程中未出現震動情況。在仿真環境中進行實驗,可避免對機械臂的損壞,為后續研究工作的順利開展提供保障。
本文將LM算法引入機械臂軌跡過程規劃,提升了軌跡規劃的精準度。與梯度下降法等傳統方法相比,梯度下降法和LM算法都可在一定時間內逼近最優解。LM算法可在更短時間內下降并得出最優解,主要由于梯度下降法容易陷入局部最優解。牛頓法因在計算過程中采用Hessian矩陣,增加了計算復雜度,而LM算法由于阻尼系數的存在,使得阻尼過大時近似梯度下降法,阻尼過小時則接近高斯牛頓法,結合了二者優點,使其成為在求解非線性最小二乘問題時較為實用的算法之一。但其受到權重參數初始化及超參數選取的影響,仍會在某些迭代時刻出現梯度上升的情況。本文在確定數學模型的基礎上,基于MATLAB構建可視化模型,并結合優化算法規劃其運動軌跡。結果表明,LM算法迭代效果良好,后續還可通過調整超參數對其作進一步改進。
參考文獻:
[1] MOHRI A, FURUNO S, YAMAMOTO M. Trajectory planning of mobile manipulator with end-effector's specified path[C]. IEEE/RSJ International Conference on Intelligent Robots & Systems, 2001:2264-2269.
[2] SHARIATI-NIA M,GHAYOUR M,MOSAYEBI M . Optimal trajectory planning of a mobile robot with spatial manipulator for obstacle avoidance[C]. Gyeonggi-do:International Conference on Control, Automation and Systems, 2010.
[3] OHTA K,SVININ M M,LUO Z W,et al. Optimal trajectory formation of constrained human arm reaching movements[J]. Biological Cybernetics,91(1):23-36.
[4] 田海波, 馬宏偉, 魏娟. 串聯機器人機械臂工作空間與結構參數研究[J]. 農業機械學報, 2013, 44(4):196-201.
[5] 姜宏超, 劉士榮, 張波濤. 六自由度模塊化機械臂的逆運動學分析[J]. 浙江大學學報(工學版), 2010(7):1348-1354.
[6] 孫亮, 馬江, 阮曉鋼. 六自由度機械臂軌跡規劃與仿真研究[J]. 控制工程,2010(3):388-392.
[7] DEAN-LEON E,NAIR S, KNOLL A. User friendly Matlab-toolbox for symbolic robot dynamic modeling used for control design[C].IEEE International Conference on Robotics & Biomimetics,2012:2081-2088.